Did you know that majority agreement isn’t required by Paxos?
In fact, most of the time, the sets of nodes required to participate in agreement (known as quorums) do not even need to intersect with each other.
This is the observation which is made, proven and realised in our latest paper draft, Flexible Paxos: Quorum Intersection Revisited. A draft of which is freely available on ArXiv.
The paper provides the theoretical foundation of the result, as well as the formal proof and a discussion of the wide reaching implications. However, in this post I hope to give a brief overview of the key finding from our work and how it relates to modern distributed systems. I’d also recommend taking a look at A More Flexible Paxos by Sugu Sougoumarane.
Background
Paxos is an algorithm for reaching distributed agreement. Paxos has been widely utilized in production systems and (arguably) forms the basis for many consensus systems such as Raft, Chubby and VRR. In this post, I will assume that the reader has at least some familiarity with at least one consensus algorithm (if not, I would suggest reading either Paxos made moderately complex or the Raft paper).
For this discussion, we will consider Paxos in the context of committing commands into a log which is replicated across a system of nodes.
The basic idea behind Paxos is that we need two phases to commit commands:
- Leader election – The phase where one node essentially takes charge of the system, we call this node the “leader”. When this node fails, then the system detects this and we choose another node to take the lead.
- Replication – The phase where the leader replicates commands onto other nodes and decides when it is safe to call them “committed”.
The purpose of the leader election phase is twofold. Firstly, we need to stop past leaders from changing the state of the system. Typically, this is done by getting nodes to promise to stop listening to old leaders (e.g. in Raft, a follower updates its term when it receives a RequestVotes for a higher term). Secondly, the leader needs to learn all of the commands that have been committed in the past (e.g. in Raft, the leader election mechanism ensures that only nodes with all committed entries can be elected).
The purpose of the replication phase is to copy commands onto other nodes. When sufficient copies of a command have been made, the leader considers the request to be committed and notifies the interested parties (e.g. in Raft, the leader applies the command locally and updates its commit index to notify the followers in the next AppendEntries).
We refer to the nodes who are required to participate in each phase as the “quorum”. Paxos (and thus Raft) uses majorities for both leader election and replication phases.
The key observation
The guarantee that we make is that once a command is committed, it will never be overwritten by another command. To satisfy this, we must require that the quorum used by the leader election phase will overlap with the quorums used by previous replication phase(s). This is important as it ensures that the leader will learn all past commands and past leaders will not be able to commit new ones.
Paxos uses majorities but there are many other ways to form quorums for these two phase and still meet this requirement. Previously, it was believed that all quorums (regardless of which phase they are from) needed to intersect to guarantee safety. Now we know that this need not be the case. It is sufficient to ensure that a leader election quorum will overlap with replication phase quorums.
In the rest of this post, we will explore a few of the implication of this observation. We will focus on two dimensions: (1) how can we improve the steady state performance of Paxos? (2) how can we improve the availability of Paxos?
Improving the performance of Paxos
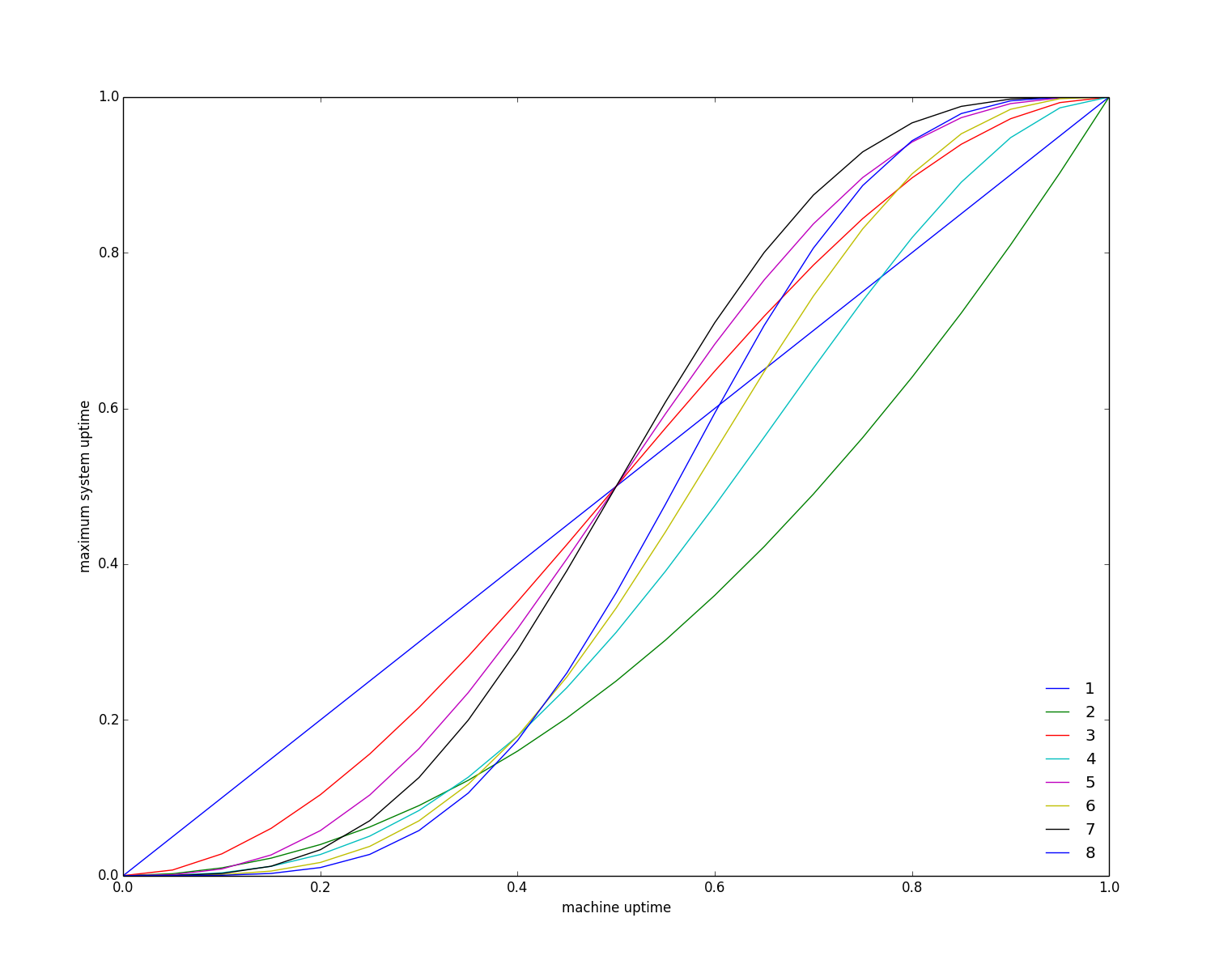
We can now safely tradeoff quorum size in the leader election phase for the quorum size in the replication phase. For example, in a system of 6 nodes, it is sufficient to get agreement from only 3 nodes in the replication phase when using majorities for leader election. Likewise, it is sufficient to get agreement from only 2 nodes in the replication phase if you require that 5 nodes participate in leader election.
Reducing the number of nodes required to participate in the replication phase will improve performance in the steady state as we have fewer nodes to wait upon and to communicate with.
But wait a second, isn’t that less fault tolerant?
Firstly, we never compromise safety, this is a question of availability. It is here that things start to get really interesting.
Let’s start by splitting availability into two types: The ability to learn committed commands and elect a new leader (leader election phase) and the ability for the current leader to replicate commands (replication phase).
Why split them? Because both of these are useful in their own right. If the current leader can commit commands but we cannot elect a new leader then the system is available until the current leader fails. If we can elect a new leader but not commit new commands then we can still safely learn all previously committed values and then use reconfiguration to get the system up and running again.
In the first example, we used replication quorums of size n/2 for a system of n nodes when n was even. This is actually more fault-tolerant than Paxos. If exactly n/2 failures occur, we can now continue to make progress in the replication phase until the current leader fails.
For different quorum sizes, we have a trade off to make. By decreasing the number of nodes in the replication phase, we are making it more likely that a quorum for the replication phase will be available. However, if the current leader fails then it is less likely that we will be able to elect a new one.
The story does not end here however.
We can be more specific about which nodes can form replication quorums so that it is easier to intersect with them. For example, if we have 12 nodes we can split them into 4 groups of 3. We could then say that a replication quorum must have one node from each group. Then when electing a new leader, we need only require any one group to agree. This is shown in the picture below, on the left we simply count the number of nodes in a quorum and on the right we use the groups as described.
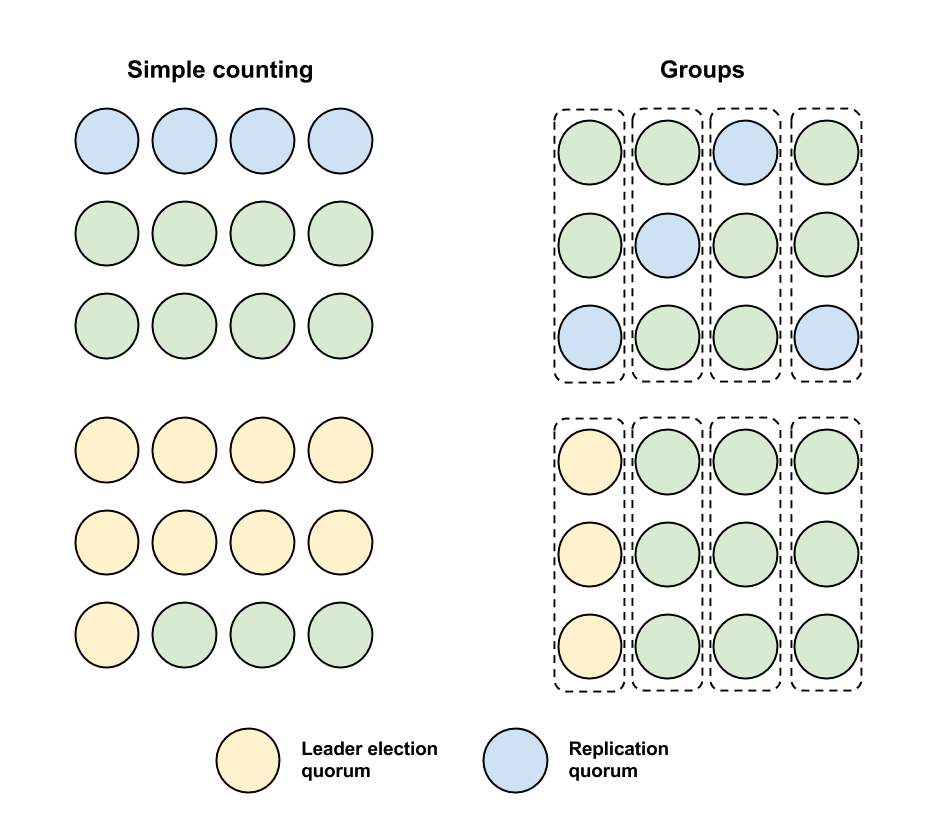
It is the case in both examples that 4 failures could be sufficient to make the system unavailable if the leader also fails. However, with groups is not the case that any 4 failures would suffice, now only some combinations of node failures are sufficient (e.g. one failure per group).
There is a host of variants on this idea. There are also many other possible constructions. The key idea is that if we have more information about which nodes have participated in the replication phase then it is easier for the leader election quorums to intersect with replication quorums.
We can take this idea of being more specific about which nodes participate in replication quorums even further. We could extend the consensus protocol to have the leader notify the system of its choice of replication quorum(s). Then, if the leader fails, the new leader need only get agreement from one node in each possible replication quorum from the last leader to continue.
No matter which scheme we use for constructing our quorums and even if we extend our protocol to recall the leader’s choice of quorum(s), we always have a fundamental limit on availability. If all nodes in the replication quorum fail and so does the leader then the system will be unavailable (until a node recovers) as no one will know for sure what the committed command was.
Improving the availability of Paxos
So far, we have focused on using the observation to reduce the number of nodes required to participate in the replication phase. This might be desirable as it improves performance in the steady state and makes Paxos more scalable across a larger number of nodes.
However, it is often the case that availability in the face of failure is more important than steady state performance. It may also be the case that a deployment only has a few nodes to utilise.
We can apply this observation about Paxos the other way around. We can increase the size of the replication quorum and reduce the size of the quorum for leader election. In the previous example, we could use 2 nodes per group for replication then only requiring 2 nodes for any group for leader election.
Returning to the trade off from before. By increasing the number of nodes in the replication phase, we are making it more likely that we will be able recover when failures occurs. However, we increase the chance of a situation where we have enough nodes to elect a leader but we do not have enough nodes to replicate. This is still useful as if we can elect a leader then we can reconfigure to remove/replace the nodes.
At the extreme end, we can require that all nodes participate in replication and then only one node needs to participate in leader election. Assuming we can handle the reconfiguration, we can now handle F failures using only F+1 nodes.
Conclusion
Paxos is a single point on a broad spectrum of possibilities. Paxos and its majority quorums is not the only way to safely reach consensus. Furthermore, the tradeoff between availability and performance provided by Paxos might not be optimal for most practical systems.
Caveats
There are as always many caveats and we refer to the paper for a more formal and detailed discussion.
- If this result is applied to Raft consensus, we do still need leader election quorums to intersect. This is because Raft uses leader election intersect to ensure that each term is used by at most one leader. This is specific to Raft and is not true more generally.
- This is far from the first time that it has been observed that Paxos can operate without majority. However, previously it was believed that all quorums (regardless of which of the phases they were from) needed to intersect. This fundamentally limits the performance and availability of any scheme for choosing quorums and is probably why we do not really see them used in practice.
Acknowledgments
During the preparation of our paper, Sugu Sougoumarane released a blog post, which explains for a broad audience some of the observations on which this work is based.
`The most useful piece of learning for the uses of life is to unlearn what is untrue. ” Antisthenes