TL;DR: Run distributed systems using majority quorum on an odd number of machines.
Paxos, Raft, Viewstamped Replication and many other consensus algorithms operate on majority quorums. A majority quorum is any subset of nodes containing at least a strict majority of nodes. These algorithms all require a majority quorum to agree to a value before its considered to be committed. This ensures that any agreement will be aware of all past agreements, as there will always be in intersection of at least one mode between any two majority quorums.
It is a prerequisite that at least a strict majority of nodes are up for the system using these consensus protocols to be operational. From this, we can establish an upper bound on the uptime of any system using majority quorum consensus. For this calculation, we assume node failures are independent. Whilst this is a fair assumption, it is of course not the case in practice.
We can calculate the probability that a strict majority of node are up as follows:
p is the probably that a node is live, n is number of nodes and underline means floor.
This equation is also the CDF of the Binomial distribution. It works by summing up the probability what no nodes are down, only one node is down, two nodes are down etc.. until you reach the case where the largest possible minority of nodes are down.
The following graph shows the relationship between node uptime p and majority quorum uptime (each line represent the number of nodes from 1 to 8):
A system with two nodes is more likely to fail than a system with one. It’s easy to see why this is. If either node in a system of two machines fails then the system is down (as its unable to get a strict majority). Since there are two node instead of one, a failure is likely to occur. In other words, the probably of a system of one node having a majority is p, whilst for a system of two nodes its p^2.
If node uptime is less than half, your best off with only one node. In practice, your best off with not using majority quorum consensus.
Adding a node to an odd set of nodes doesn’t improve uptime. Adding this extra node doesn’t increase the number of failures that can we handled, e.g. 5 nodes can handle upto two failures and 6 nodes can also only handle upto two failures. The summation above has no extra terms in this case but the existing terms are smaller as p is raised to a higher power.
This approach is of course very limited. We are not accounting for how extra nodes aid in the handling of read-only commands, the duration and pattern of failures and that machine failures are not independent.
I assume this is well known result in the theory of distributed system but I’ve not come across it before. If anyone has seen it before, I can you send me a pointer to the work.
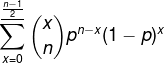
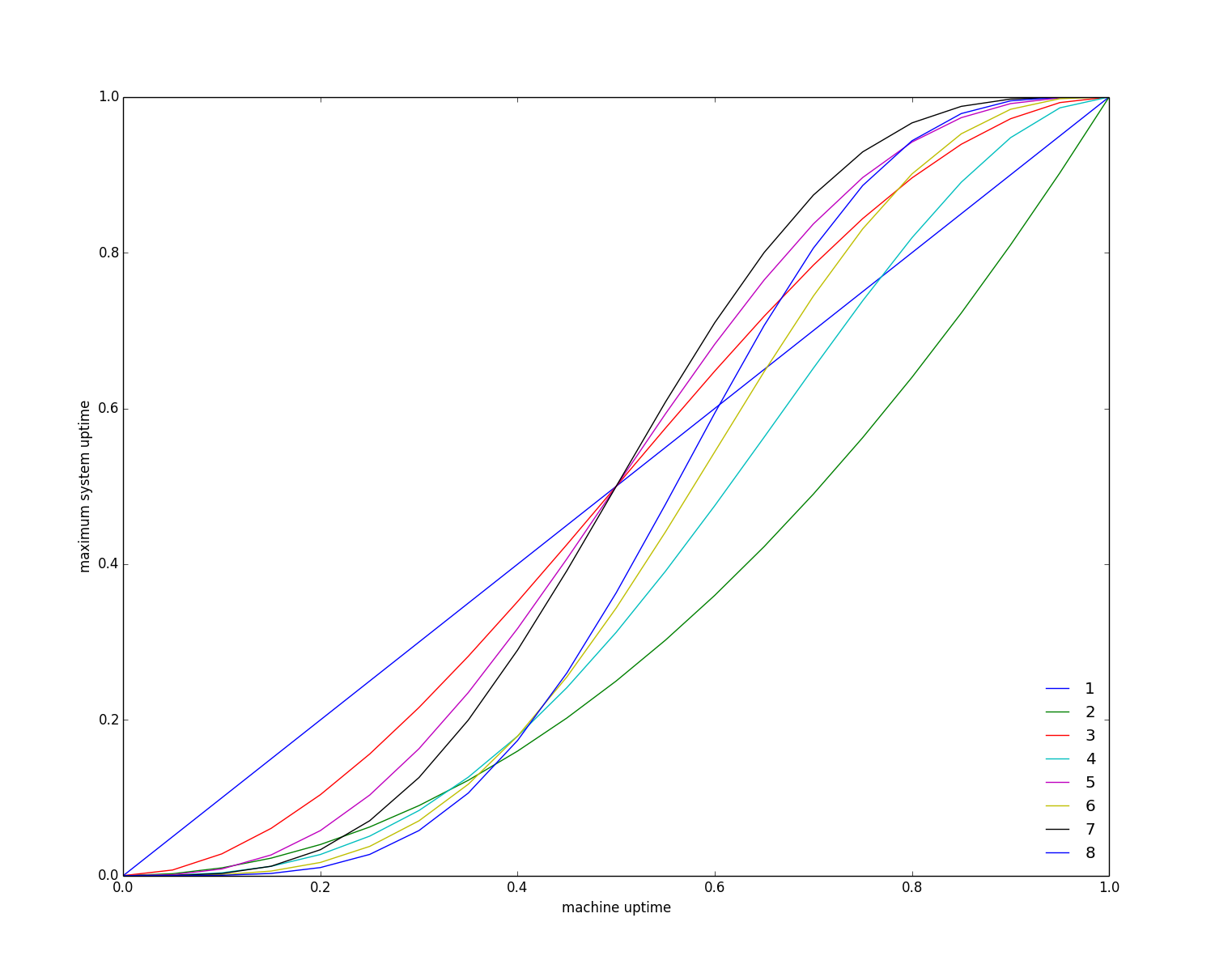
In mission critical distributed systems, unavailability is typically not an option. Typical resilience goals might be three nines after the dot, six nines in extremely crucial settings, and so on. So the really interesting part is the top right corner, where individual component failures may give you only one or two nines guarantee, i.e., p=.9 or p=.99; in this zone, quorums boost the resilience significantly.
Note that, most of the area in the graph intuitively follows from simply observing that the expected number of failures (1-p)*n is more than the resilience bound.
A very old starting point where quorum systems have been evaluated is: Y. Amir and A. Wool. Evaluating quorum systems over the Internet. In Proc. 26’th IEEE Symp. Fault-Tolerant Computing (FTCS), pages 26–35, Sendai, Japan, 1996.